それでは、前記事で紹介したヒント材料の、
「図」「金庫の番号に関するメモ」から、まず数字の正体を探りましょう。
「図」を見ると、なんだか見覚えのある渦巻きに、
それぞれのマス目にピン留めされ、赤いヒモの先に数字がふられています。
また、離れたところに単独で011と書かれています。
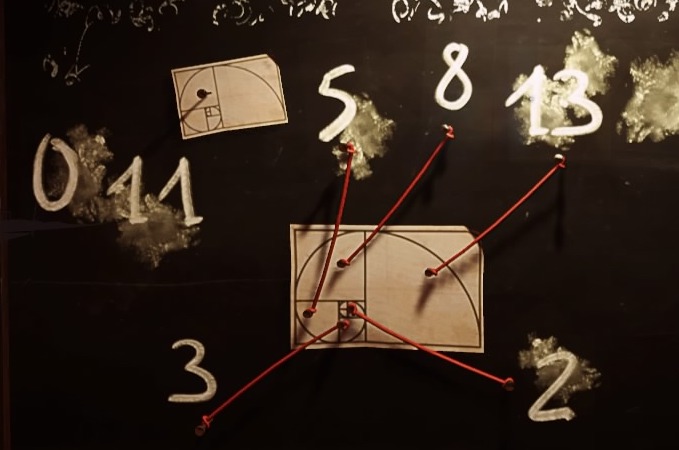
そう、この渦巻きは美術やデザインの授業で習ったかもしれない、人間が見て
美しいと感じる対比率といわれている「黄金比」の左右反転バージョンです。
(黄金比の参考文献:photoshopvip.net)
そして、そのそばに貼られていた手紙「金庫の番号に関するメモ」を読むと、

「数列か?番号のどれもが素数ってわけじゃないな・・」と言っている通り、
素数(約数が2つしかない数字)だと、2,3,5,7,11,13,17,29...になるので、
「図」の数字は素数ではありませんが、それとは別の数学的な「数列」であること
が推察できます。
「数列」「どの番号もその前の番号から生成されている」という言葉を気にしなが
ら、黄金比サイトにあったマス目に黄金比率(数字)をふった図をみてみると、
前の数字を足した数が次の数字になっていることに気づきました。
↓説明用に自作した図ががこちら。(ゲームの「図」とは左右反転です)
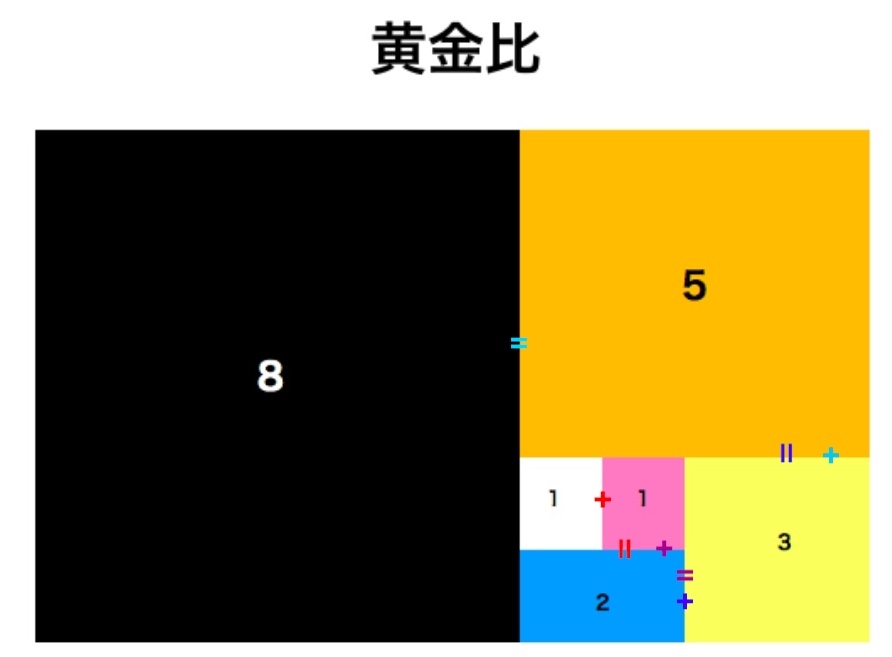
渦巻きの中心から反時計回り
(ピンク・白・青・黄・オレンジ・黒)にみていくと、
1(ピンク)+1(白)=2(青) *自作の図は赤=と紫+の位置が間違ってます。
1(白)+2(青)=3(黄)
2(青)+3(黄)=5(オレンジ)...というように、
「前の番号から生成されいている」ことがわかります。
この法則にしたがって全部の金庫解錠に必要な15の数字
(次の記事で詳しく紹介)になるまで計算しましょう。
↓(私がプレイ中に書いたメモ)
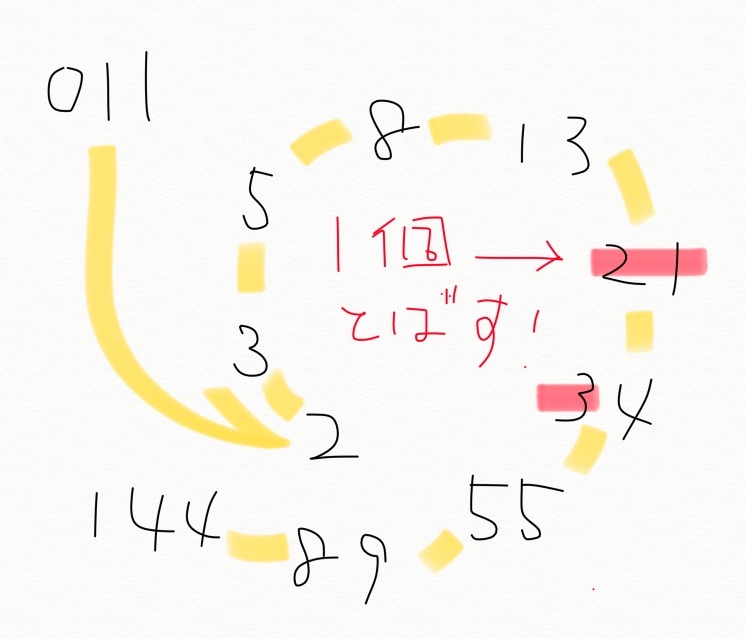
*追記===============================
プレイ中は自力で足し算して解錠したのですが、
今回記事を書くにあたってあらためて調べたところ、
それが『フィボナッチ数列』だったことがわかり、
計算しなくても数字、早わかりしちゃうんですよね…。
でも自分で計算して出した方がダントツで達成感があるので、
できれば一度計算して楽しんでほしいな〜と思います。
ちなみにWatchdogsでもプレイ中、
フィボナッチ数列って出てきたので、
ゲーム製作者お気に入りの数列なのかもしません。
↓(フィボナッチ数列について)
黄金比を調べると『フィボナッチ数列』との関連性に触れており、
(フィボナッチ数列の隣同士の数の比をとると、その比が次第に黄金比に近づいていく)
『フィボナッチ数列』とは、
”3項目以降のそれぞれの数は手前の2つの項の数の和になっている”
0,1,1,2,3,5,8,13,21,34,55,89,144,233...
すなわち、手紙にある「数列」「どの番号もその前の番号から生成されている」は、
『フィボナッチ数列』であり、さらに手紙に書かれてある
「金庫の番号をすべて一つの長い列にまとめる必要があるな」から、
図にふられていた数字は、
01123581321345589144...とカンマなしに並べていいことがわかります。
「図」「金庫の番号に関するメモ」から、まず数字の正体を探りましょう。
「図」を見ると、なんだか見覚えのある渦巻きに、
それぞれのマス目にピン留めされ、赤いヒモの先に数字がふられています。
また、離れたところに単独で011と書かれています。
そう、この渦巻きは美術やデザインの授業で習ったかもしれない、人間が見て
美しいと感じる対比率といわれている「黄金比」の左右反転バージョンです。
(黄金比の参考文献:photoshopvip.net)
そして、そのそばに貼られていた手紙「金庫の番号に関するメモ」を読むと、
「数列か?番号のどれもが素数ってわけじゃないな・・」と言っている通り、
素数(約数が2つしかない数字)だと、2,3,5,7,11,13,17,29...になるので、
「図」の数字は素数ではありませんが、それとは別の数学的な「数列」であること
が推察できます。
「数列」「どの番号もその前の番号から生成されている」という言葉を気にしなが
ら、黄金比サイトにあったマス目に黄金比率(数字)をふった図をみてみると、
前の数字を足した数が次の数字になっていることに気づきました。
↓説明用に自作した図ががこちら。(ゲームの「図」とは左右反転です)
渦巻きの中心から反時計回り
(ピンク・白・青・黄・オレンジ・黒)にみていくと、
1(ピンク)+1(白)=2(青) *自作の図は赤=と紫+の位置が間違ってます。
1(白)+2(青)=3(黄)
2(青)+3(黄)=5(オレンジ)...というように、
「前の番号から生成されいている」ことがわかります。
この法則にしたがって全部の金庫解錠に必要な15の数字
(次の記事で詳しく紹介)になるまで計算しましょう。
↓(私がプレイ中に書いたメモ)
*追記===============================
プレイ中は自力で足し算して解錠したのですが、
今回記事を書くにあたってあらためて調べたところ、
それが『フィボナッチ数列』だったことがわかり、
計算しなくても数字、早わかりしちゃうんですよね…。
でも自分で計算して出した方がダントツで達成感があるので、
できれば一度計算して楽しんでほしいな〜と思います。
ちなみにWatchdogsでもプレイ中、
フィボナッチ数列って出てきたので、
ゲーム製作者お気に入りの数列なのかもしません。
↓(フィボナッチ数列について)
黄金比を調べると『フィボナッチ数列』との関連性に触れており、
(フィボナッチ数列の隣同士の数の比をとると、その比が次第に黄金比に近づいていく)
『フィボナッチ数列』とは、
”3項目以降のそれぞれの数は手前の2つの項の数の和になっている”
0,1,1,2,3,5,8,13,21,34,55,89,144,233...
すなわち、手紙にある「数列」「どの番号もその前の番号から生成されている」は、
『フィボナッチ数列』であり、さらに手紙に書かれてある
「金庫の番号をすべて一つの長い列にまとめる必要があるな」から、
図にふられていた数字は、
01123581321345589144...とカンマなしに並べていいことがわかります。
PR
COMMENT
カレンダー
| 06 | 2025/07 | 08 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
カテゴリー
最新記事
(12/30)
(07/23)
(07/23)
(07/18)
(07/06)
ブログ内検索
プロフィール
HN:
solex
性別:
非公開
職業:
会社員
趣味:
ゲーム、読書、ヨガ、音楽鑑賞
自己紹介:
中小企業にて働く普通の会社員。仕事優先で生きてます。
多忙と眼精疲労からくる頭痛で
長時間ゲームができず、
すっかりブログが停滞中。
多忙と眼精疲労からくる頭痛で
長時間ゲームができず、
すっかりブログが停滞中。
忍者アナライズ

